COSMIC SECRETS, PART 2
This page represents a continuation of the "Democracy" page of this website. The "Democracy" page concluded by mentioning how everything in the Universe is relative including age and weight. As mentioned on the "Democracy" page, some readers might be wondering the following: How is that someone who weighs, say, 100 pounds (45 kilograms) on Earth would only weigh the equivalent of 7 pounds (3 kilograms) on Pluto. How is it that someone who is, say, 50 years old on Earth would only be the equivalent of 0.201 of a year old on Pluto?
The answers to both of these questions go back to Sir Isaac Newton and his law of universal gravitation. The "Cosmic Secrets" page of this website provided a brief and partial illustration of both Johannes Kepler's third law of planetary motion and Sir Isaac Newton's law of universal gravitation. Sir Isaac Newton's law of universal gravitation, among other things, offered an alternate proof for Johannes Kepler's third law of planetary motion.
THE PARADOX OF WEIGHT
Take the paradox of weight, for instance. Sir Isaac Newton's law of universal gravitation states that weight actually should be viewed as a force. Sir Isaac Newton's formula for force (weight) is written as follows:
F=m × a
Where,
- F = Force of gravity attracting one object to another object (unknown value)
- m = mass of object
- a = gravity's acceleration rate (for example, 9.80665 meters per second squared on Earth)
The product of this force is referred to as newtons.
Humans are composed of matter. The amount of matter in an object is known as its mass. In the metric system, a basic unit of mass is known as the gram. (Grams are equivalent to ounces in USA measurement units.) And 1,000 grams are equal to 1 kilogram. (Kilograms are equivalent to pounds in USA measurement units, and 1 kilogram is equivalent to 2.20462262 pounds.)
According to Sir Isaac Newton's law, your mass would not change if you relocated from, say, Earth to Pluto—or any other heavenly body. Your weight, however, would change. Your weight would be equivalent to an object's mass under the influence of the force of gravity, hence, variable F in the F=m × a formula. Mass accelerates towards the center of gravity. The formal term to represent mass's acceleration under the influence of gravity is called the newton. (One kilogram of mass is equivalent to 9.80665 newtons.)
Scientists already have computed the acceleration of gravity (that is, variable a in the F=m × a formula) at or near Earth's surface to be 9.80665 meters per second squared, which is sometimes rounded to 10 m/s² to simplify the computation. To determine your weight on another heavenly body, it becomes a matter of (a) determining the conversion factor from Earth's acceleration rate to the heavenly body's acceleration rate, (b) substituting the value for mass (that is, your or anyone's weight on Earth), and (c) multiplying your weight by the conversion factor to determine your weight on the heavenly body. The first table below (Leaving Planet Earth: Weight) illustrates how this weight computational procedure is performed.
| Heavenly Body | Acceleration of Gravity (m/s²) | Gravity's Acceleration on Earth | Acceleration Conversion Factor Relative to Earth | Weight (Example) | Unknown (Equivalent Weight On Heavenly Body) |
|---|---|---|---|---|---|
| Mercury | 3.7 | 9.80665 | 0.377294999 | 100 | 37.7 |
| Venus | 8.87 | 9.80665 | 0.904488281 | 100 | 90.4 |
| Earth | 9.80665 | 9.80665 | 1 | 100 | 100.0 |
| Moon | 1.62 | 9.80665 | 0.165194027 | 100 | 16.5 |
| Mars | 3.71 | 9.80665 | 0.378314715 | 100 | 37.8 |
| Jupiter | 24.79 | 9.80665 | 2.527876492 | 100 | 252.8 |
| Saturn | 10.44 | 9.80665 | 1.064583726 | 100 | 106.5 |
| Uranus | 8.87 | 9.80665 | 0.904488281 | 100 | 90.4 |
| Neptune | 11.15 | 9.80665 | 1.136983577 | 100 | 113.7 |
| Pluto | 0.58 | 9.80665 | 0.05914354 | 100 | 5.9 |
| DATA SOURCE FOR ACCELERATION: http://nssdc.gsfc.nasa.gov/planetary/planetfact.html | |||||
Using Pluto as an example, the table above shows that dividing 0.58 (Pluto's gravitational acceleration rate according to the fact sheet) by Earth's gravitational acceleration rate (9.80665) yields a conversion factor of 0.05914354. That is to say, one newton on Earth is equivalent to 0.05914354 of a Newton on Pluto. Next, multiplying your weight times the conversion factor gives your weight on Pluto. The table above uses a sample weight of 100 pounds. When multiplying 100 pounds times the conversion factor of 0.05914354, the weight on Pluto becomes 5.9 or 6 pounds. (You'll notice that the "Democracy" page stated that your weight on Pluto would be 7 pounds instead of 6 pounds. The discrepancy is explained by the fact that a web calculator was used to perform the computation on the "Democracy" page. It so happens that the web calculator uses a rounded gravitational acceleration rate of 10 meters per second squared on Earth and a 0.67 acceleration rate for Pluto. The above table uses a 9.80665 acceleration rate for Earth and a 0.58 acceleration rate for Pluto.)
But, how is the acceleration rate due to gravity determined for any given heavenly body (that is, variable a in the F=m × a formula)? The answer goes back to Sir Isaac Newton law of universal gravitation. The law of universal gravitation states that every object throughout the Universe is attracted to every other object. The force of attraction between objects is directed along the line of centers of those objects. The strength or magnitude of the attraction between those objects is proportional to the product of their masses and is inversely proportional to the square of the distance between them. Sir Isaac Newton's law of universal gravitation can be expressed as follows:
Where,
- Fg = Force of gravity attracting one object to another object (unknown value)
- G = Gravitational constant (6.67428 × 10⁻¹¹ m³ kg⁻¹ s⁻²)
- ma = mass of object a
- mb = mass of object b
- r = radius, or distance between two objects, a and b, as measured from their center points
It should be noted that 9.80665 meters per second squared is used as the official value for variable a at or near the Earth's surface. Earth's gravitational acceleration rate of 9.80665 meters per second squared has been adopted by all global measurement bodies such as the USA's Department of Commerce and its National Institute of Standards and Technology (NIST).
Based on Sir Isaac Newton's law of universal gravitation, gravity's acceleration value at or near Pluto's surface (0.61 m/s²) can be derived by using the following formula:
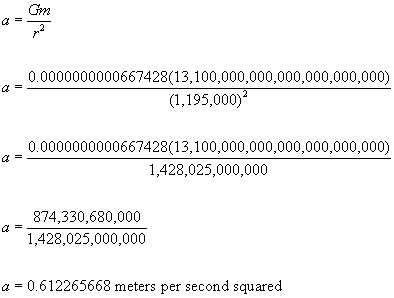
Where,
- a = acceleration due to the force of gravity (unknown value)
- G = Gravitational constant (6.67428 × 10⁻¹¹ m³ kg⁻¹ s⁻²)
- m = mass of Pluto (0.0131 × 10²⁴ kg or 13,100,000,000,000,000,000,000 kilograms)
- r = radius of Pluto (1,195 kilometers or 1,195,000 meters)
Notice how the fact sheet in the above table gives a gravitational acceleration rate of 0.58 meter per second squared for Pluto. The above formula gives a gravitational acceleration rate of 0.61 meter per second squared. Much like the 6 and 7 pound weight discrepancies mentioned above, here's another instance of a discrepancy in computed values for the same phenomenon. In this instance, the discrepancy is due to different values used for Pluto's mass and radius. Obviously, scientific opinions are evolving regarding Pluto's mass. The slight difference in values (that is, 0.58 versus 0.61) would not significantly alter your computed weight on Pluto compared to your weight on Earth.
The solution to the weight paradox is this: The effect of weight is larger on heavenly bodies with higher gravitational rates because the force being exerted is stronger. The closer the force of gravity reaches a value of zero, then the more you would experience the effect of zero weight or weightlessness.
THE PARADOX OF AGE
Take the paradox of age, for instance. Age is measured in terms of units of time. Two ways to measure age on Earth are by days and by years. A day is measured by the length of time it takes the Earth to make a complete 360-degree revolution on its axis, which is 24 hours. It also takes the Earth a little over 365 days to make a complete orbit of the Sun, which is a year. If the Earth has made, say, 50 complete orbits of Sun during your lifetime, then it would be stated that you have lived for 50 (Earth) years.
Scientists have determined that it takes Pluto the equivalent of 153 hours to make a complete 360-degree revolution on its axis. Therefore, as shown in the first table below, a day on Earth would be equivalent to 0.156135839 of a day on Pluto (that is, Earth's rotation ÷ Pluto's rotation).
The next table below (Leaving Planet Earth: Age as Days) illustrates a day on Earth, age (as days), and their equivalents in the Solar System.
| Heavenly Body | Rotation Period (hours) | Hours to Day | Orbital Period (days) | Days to Year | Days Conversion Factor Relative to Earth | Equivalent Elapsed Days Relative to 365.256 Elapsed Days on Earth | Age (Example) | Unknown (Equivalent Elapsed Days on Heavenly Body Per Earth Age) |
|---|---|---|---|---|---|---|---|---|
| Mercury | 1407.6 | = 1 Day | 87.969 | = 1 Year | 0.017003765 | 6.210727289 | 50 | 310.5363645 |
| Venus | -5832.6 | = 1 Day | 224.701 | = 1 Year | -0.004103573 | -1.498854667 | 50 | -74.94273336 |
| Earth | 23.9345 | = 1 Day | 365.256 | = 1 Year | 1 | 365.256 | 50 | 18262.8 |
| Moon | 23.9345 | = 1 Day | 365.256 | = 1 Year | 1 | 365.256 | 50 | 18262.8 |
| Mars | 24.6229 | = 1 Day | 686.98 | = 1 Year | 0.972042286 | 355.0442772 | 50 | 17752.21386 |
| Jupiter | 9.925 | = 1 Day | 4,332.59 | = 1 Year | 2.411536524 | 880.8281846 | 50 | 44041.40923 |
| Saturn | 10.656 | = 1 Day | 10,759.22 | = 1 Year | 2.24610548 | 820.4035034 | 50 | 41020.17517 |
| Uranus | -17.24 | = 1 Day | 30,685.40 | = 1 Year | -1.388312065 | -507.0893116 | 50 | -25354.46558 |
| Neptune | 16.11 | = 1 Day | 60,189 | = 1 Year | 1.485692117 | 542.6579598 | 50 | 27132.89799 |
| Pluto | -153.2928 | = 1 Day | 90,465 | = 1 Year | -0.156135839 | -57.02955215 | 50 | -2851.477608 |
| DATA SOURCE FOR ROTATION PERIOD: http://nssdc.gsfc.nasa.gov/planetary/planetfact.html | ||||||||
Scientists also have determined that it takes Pluto 248 years to make a complete orbit of the Sun. To determine your age on another heavenly body, it becomes a matter of (a) determining the conversion factor from Earth's orbital period to the heavenly body's orbital period, (b) substituting your age into the equation (that is, your age or anyone's age on Earth), and (c) multiplying your age by the conversion factor to determine your age on the heavenly body. The next table (Leaving Planet Earth: Age as Years) illustrates how this age computational procedure is performed.
| Heavenly Body | Orbital Period (days) | Days to Year | Equivalent Orbital Period (years) | Earth's Orbital Period (days) | Year Conversion Factor Relative to Earth | Age (Example) | Unknown [Equivalent Age on Heavenly Body (years old)] |
|---|---|---|---|---|---|---|---|
| Mercury | 87.969 | = 1 Year | 0.24084204 | 365.256 | 4.152099035 | 50 | 207.6049517 |
| Venus | 224.701 | = 1 Year | 0.615187704 | 365.256 | 1.625520136 | 50 | 81.27600678 |
| Earth | 365.256 | = 1 Year | 1 | 365.256 | 1 | 50 | 50 |
| Moon | 365.256 | = 1 Year | 1 | 365.256 | 1 | 50 | 50 |
| Mars | 686.98 | = 1 Year | 1.880817837 | 365.256 | 0.531683601 | 50 | 26.58418003 |
| Jupiter | 4,332.59 | = 1 Year | 11.86178735 | 365.256 | 0.084304327 | 50 | 4.215216352 |
| Saturn | 10,759.22 | = 1 Year | 29.45665506 | 365.256 | 0.033948186 | 50 | 1.697409292 |
| Uranus | 30,685.40 | = 1 Year | 84.01066649 | 365.256 | 0.01190325 | 50 | 0.59516252 |
| Neptune | 60,189 | = 1 Year | 164.7857941 | 365.256 | 0.006068484 | 50 | 0.303424214 |
| Pluto | 90,465 | = 1 Year | 247.6756029 | 365.256 | 0.004037539 | 50 | 0.201876969 |
| DATA SOURCE FOR ORBITAL PERIOD: http://nssdc.gsfc.nasa.gov/planetary/planetfact.html | |||||||
Again, using Pluto as an example, the above table (Leaving Planet Earth: Age as Years) shows that dividing the Earth's orbital period (that is, 365.256 days) by Pluto's orbital period in days (that is, 90,465 days) gives a conversion factor of 0.004037539. That is to say, one year on Earth is equivalent to 0.004037539 of a year on Pluto. Next, multiplying your age times the conversion factor gives your age on Pluto. The table above uses a sample age of 50 years old. When multiplying 50 years times the conversion factor of 0.004037539, your age on Pluto becomes 0.201876969 of a year old. In other words, 50 Earth years are only equivalent to 0.201 of a Pluto year. Instead of speaking in terms of 24 hours a day and 365 days a year, on Pluto, you would speak of 153 hours a day and 90,465 days a year.
But, how is the heavenly body's orbital period determined? The answer goes back to Johannes Kepler's third law of planetary motion. Johannes Kepler's third law of planetary motion states that, for planets orbiting the Sun, the square of the time that it takes a planet to orbit of the Sun is equal to the cube of its distance from the Sun.
Pluto's orbital period is computed below to illustrate Johannes Kepler's third law of planetary motion.
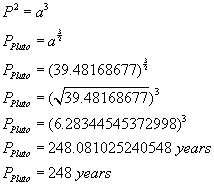
Where,
- P = period of time it takes the planet to orbit the Sun as computed on Earth
- a = length of the planet's semimajor axis relative to Earth, or the planet's equivalent astronomical units relative to Earth
Based on its average distance from the Sun, Johannes Kepler's formula reveals that it takes Pluto 248 years to make a 360-degree orbit the Sun.
Johannes Kepler's formula for orbital periods was refined by Sir Isaac Newton. The refined formula typically is written as follows:

Where,
- P = period of time it takes the planet to orbit the Sun as computed on Earth (unknown value)
- π or pi = 3.14159265
- R = (Pluto's) average distance from Sun or semimajor axis (5,906.38 × 10⁶ kilometers or 5,906,380,000,000 meters for Pluto)
- G = Gravitational constant (6.67428 × 10⁻¹¹ m³ kg⁻¹ s⁻²)
- M = mass of Sun (1,988,500 × 10²⁴ kg)
The solution to the age paradox is this: In a Solar System-like scenario whereby all heavenly bodies in the system are anchored to a dominant star such as the Sun by the force of gravity, time, as measured in orbits of the Sun, moves more slowly the farther the heavenly body is positioned away from the star (Sun). As a result, your age would increase at a slower rate the farther from the Sun that you are positioned in the system.
FATE OF THE EARTH: A PESSIMISTIC VIEW
What is the fate of the Earth? What is the fate of humankind? There is no shortage of doomsday scenarios to depict the end of time for Earth and its human inhabitants. Some of these rather horrific doomsday scenarios include:
- Humans will despoil, pollute, and mismanage the Earth's natural resources such as its air, water and land to such a detrimental extent until life on Earth no longer would be sustainable.
Watch (The Day After Tomorrow - Official Teaser)
- As the result of a major world war, that is, a ferocious and all-out
international exchange of nuclear, chemical, and biological weapons, humans, one day, will destroy their species and all other life forms on Earth.
Watch (The War Game)
- As a result of a scientific or technological endeavor that goes horribly wrong, humans, one day, will destroy their species and all other life forms on Earth.
Watch (I Am Legend - Official Trailer)
- Human reign on Earth will be ended unexpectedly by a force of Nature such as an asteroid strike, a destabilized Earth core, or a massive and lethal eruption on the Sun.
Watch (Deep Impact - Trailer)
- Human reign on Earth will be ended by an apocalypse started by God (for instance, similar to the apocalypse discussed in the Holy Bible's Book of Revelations).
Watch (2012 Trailer #1)
Watch (2012 Trailer #2)
- Human reign on Earth will be ended by a nefariously inspired extraterrestrial invasion.
Watch (Independence Day - Official Trailer 1)
- Human reign on Earth will be ended by a gargantuan cosmic explosion or a gargantuan cosmic collision. Many astronomers believe that the Milky Way galaxy will collide with the Andromeda galaxy in another 2 or 3 billion years. These astronomers believe that this type of cosmic collision could either obliterate Earth or could generate shock waves that are strong enough to cause the Earth to leave its orbit of the Sun. Under this scenario, the Earth would fly into empty space, would lose its atmosphere, would freeze, and would no longer be capable of sustaining life.
Watch [When Worlds Collide (1951) Trailer]
- Some speculate that, on a cosmic scale, perhaps the end for Earth and humans will come as a natural part of the Universe's evolution. Just as all humans eventually will die of old age one day, some believe that the Universe, too, one day will die of old age. The Universe is expected either to continue expanding forever but will eventually exhaust its energy and will simply die, or, in expanding, the Universe will become so inflated until, like an overblown balloon, it will pop (explode) and die.
Watch (The Ultimate Fate Of The Universe - Part 5)
FATE OF THE EARTH: AN OPTIMISTIC VIEW
The optimistic view of Earth's fate and the fate of humankind goes something like this: Humankind somehow will find a way to elude, escape, successfully prepare for, or avoid all of these potential doomsday scenarios of mayhem, pandemonium, calamity, and annihilation. The optimistic view is that humankind will evolve into higher consciousness and will proceed to colonize deep space on a permanent, full-time basis.
MORAL OF THE STORY
What is the moral of this age-weight paradox story? The moral is this: There is no place like home (Earth). Humans cannot simply pack up their belongings, board a spacecraft, settle on another heavenly body, and expect for life on that heavenly body to be exactly like it is on Earth. Some scientists believe that heavenly bodies similar to Earth do exist elsewhere in the Universe. However, it is a totally separate matter for humans actually to navigate across interstellar and intergalactic space to establish homes on those Earth-like heavenly bodies. Obviously, successful completion of such an interstellar or intergalactic relocation feat is far easier said than done.
In the interim, on the one hand, it seems wiser and simpler for humans to make Earth the best possible home it could be (much like Heaven) instead of them making it the worst possible home (much like Hell). Why should humans mess up the good thing that they already have going right here on Earth? For, as the saying goes, "a bird in the hand is worth two in the bush". In other words, it is infinitely easier for humans to make the most of life on Earth rather than for them to destroy Earth and then be compelled to start life anew on another heavenly body.
On the other hand, given that there are forces in Nature over which humans have little control (such as colliding galaxies and exploding stars), it seems logical for humans to start preparing a second home or for humans to start preparing backup homes in deep space. Humans would need to evolve into a different type of mindset to survive in deep space. To say it mildly, all of this warring, fighting, hatred, and humans killing one another every place on Earth everyday of the year, well, it is for the birds.
FLATTER THIS SITE:

SEARCH THIS SITE:
Intellectual Property Disclosures: All videos and songs (as well as many of the images) referenced or spotlighted throughout this website are the legal and intellectual properties of others. All content and opinions on this website (bruessard.com) are those of the author (Edward Bruessard) exclusively and do not necessarily reflect the opinions of the contributors, creators, owners, and distributors of these referenced videos, songs, and images. The author holds no legal interest or financial stake in any of these referenced videos, songs, and images. The contributors, creators, owners, and distributors of these referenced videos, songs, and images played no role at all regarding the appearance of said videos, songs, and images throughout this website; they had no clue that this website would be spotlighting their works.


