COMET HALLEY
Perhaps there is no other comet more famous than comet Halley. Although comet Halley was first observed by humans as far back as the period of time before Jesus Christ appeared on Earth well over 2,000 years ago, comet Halley was not systematically monitored until year 1607 when Johannes Kepler [born year 1571 and died year 1630 at aged 58] caught a glimpse of it through his telescope. Comet Halley was named after Sir Edmund Halley [born 1656 and died 1742 at aged 85] who observed it in year 1682. In year 1705, Sir Edmund Halley was the first person to mathematically deduce Halley's orbital period of 75 years (principally by consulting the body of scientific work promulgated by Sir Isaac Newton).
Note that the topic of orbits previously was covered on the "Cosmic Secrets 2" page of this website. As applicable to comet Halley, on average, it takes Halley about 75.3 years to make a complete orbit of the Sun. The table below outlines Halley's observed orbits around the Sun from the 17th century to the future time of year 2061. A starting point of the 17th century was selected for comet Halley's observed appearances in the table below because the 17th century marked the point in time when Halley began to be deliberately and systematically monitored.
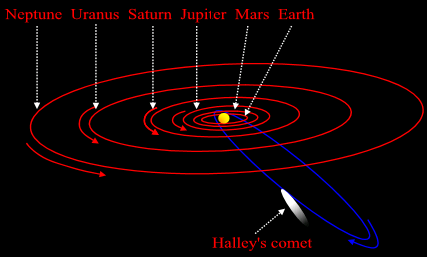
COMET HALEY RETURNS EVERY 75 OR 76 YEARS
| Dates of Halley's Perihelion or Closest Approach to Sun |
Elapsed Time Since Halley's Previous Perihelion |
| 10/27/1607 |
|
| 9/15/1682 |
74 years, 10 months, 19 days excluding the end date. |
| 3/13/1758 |
75 years, 5 months, 26 days excluding the end date. |
| 11/16/1835 |
77 years, 8 months, 3 days excluding the end date |
| 4/20/1910 |
74 years, 5 months, 4 days excluding the end date. |
| 2/9/1986 |
75 years, 9 months, 20 days excluding the end date. |
| Approximate 5/31/2061 |
75 years, 3 months, 22 days excluding the end date. |

The method to derive Halley's orbital period or its 75-year journey around the Sun, mathematically, goes back to Johannes Kepler's third law of planetary motion. Johannes Kepler's third law of planetary motion states that, for heavenly bodies in orbit of the Sun, the square of the time that it takes a heavenly body to orbit the Sun is equal to the cube of its distance from the Sun.
Using Johannes Kepler's third law of planetary motion, Halley's orbital period is computed below thanks, in large part, to scientists such as those who work at space agencies such as NASA. These scientists have computed the value for the known variable to be used in Kepler's formula. It simply reduces to a matter of substituting the known value into the equation and then working the math to solve the equation as illustrated below.
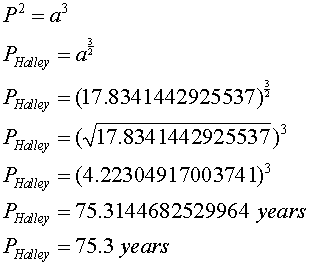
Where,
- P = period of time it takes a heavenly body (such as a planet, asteroid, or comet) to orbit the Sun as computed on Earth (unknown value)
- a = length of the Halley's semi-major axis, or the heavenly body's equivalent astronomical units from the Sun (which is the known value of 17.8341442925537 AU or 2,667,950,011.92259 kilometers for Halley)
Based on Halley's currently known average distance from the Sun (which is apt to be revised to greater precision), Johannes Kepler's formula in the above illustration reveals that it takes Halley roughly 75.3 years to complete its elliptical orbit of the Sun.
Sir Isaac Newton [born 1643 and died 1727 at aged 84] later would refine Johannes Kepler's formula for orbital periods. Sir Isaac Newton's more refined formula typically is written and derived as follows (that is, for this particular illustration of Halley's orbital period of the Sun):
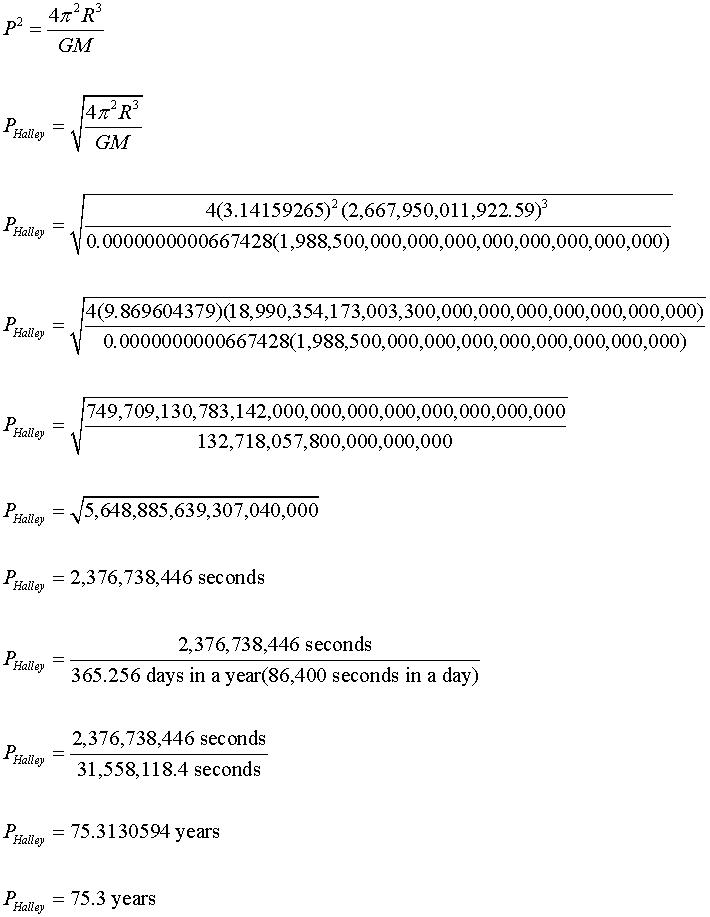
Where,
- P = period of time it takes a heavenly body (such as a planet, asteroid, or comet) to orbit the Sun as computed on Earth (unknown value)
- π or pi = 3.14159265
- R = (Halley's) average distance from Sun (2667.95001192259 × 10⁶ kilometers or 2,667,950,011,922.59 meters for Halley)
- G = Gravitational constant (6.67428 × 10⁻¹¹ m³ kg⁻¹ s⁻²)
- M = mass of Sun (1,988,500 × 10²⁴ kg)
Again, based on Halley's currently known average distance from the Sun (which is apt to be revised to greater precision), Sir Isaac Newton's formula in the above illustration reveals that it takes Halley roughly 75.3 years to complete its elliptical orbit of the Sun.
SUN / HEAVENLY BODY AVERAGE DISTANCE COMPARISONS WITH ASTRONOMICAL UNITS (AU) EQUIVALENTS
| Heavenly Body |
Average Distance from Sun (Kilometers) |
Conversion Factor (from Kilometers to Miles) |
Equivalent Average Miles from Sun (Average Distance × 0.621371192) |
Equivalent AU (Average Distance ÷ 149,597,870.7) Using Kilometers as the Base of Measure |
Equivalent AU (Average Distance ÷ 92,955,807.2375209) Using Miles as the Base of Measure |
| Earth |
149,597,871 |
0.621371192 |
92,955,807 |
1.00 |
1.00 |
| Comet Halley |
2,667,950,012 |
0.621371192 |
1,657,787,279 |
17.83 |
17.83 |
| Mercury |
57,900,000 |
0.621371192 |
35,977,392 |
0.39 |
0.39 |
| Venus |
108,200,000 |
0.621371192 |
67,232,363 |
0.72 |
0.72 |
| Mars |
227,900,000 |
0.621371192 |
141,610,495 |
1.52 |
1.52 |
| Jupiter |
778,600,000 |
0.621371192 |
483,799,610 |
5.20 |
5.20 |
| Saturn |
1,433,500,000 |
0.621371192 |
890,735,604 |
9.58 |
9.58 |
| Uranus |
2,872,500,000 |
0.621371192 |
1,784,888,749 |
19.20 |
19.20 |
| Neptune |
4,495,100,000 |
0.621371192 |
2,793,125,645 |
30.05 |
30.05 |
| Pluto |
5,906,400,000 |
0.621371192 |
3,670,066,808 |
39.48 |
39.48 |
As additional background information and as a point of reference, the above table illustrates that 1 astronomical unit (AU) is equal to 149,597,870.7 kilometers or 92,955,807.2 miles, which is the average distance from Earth to the Sun.
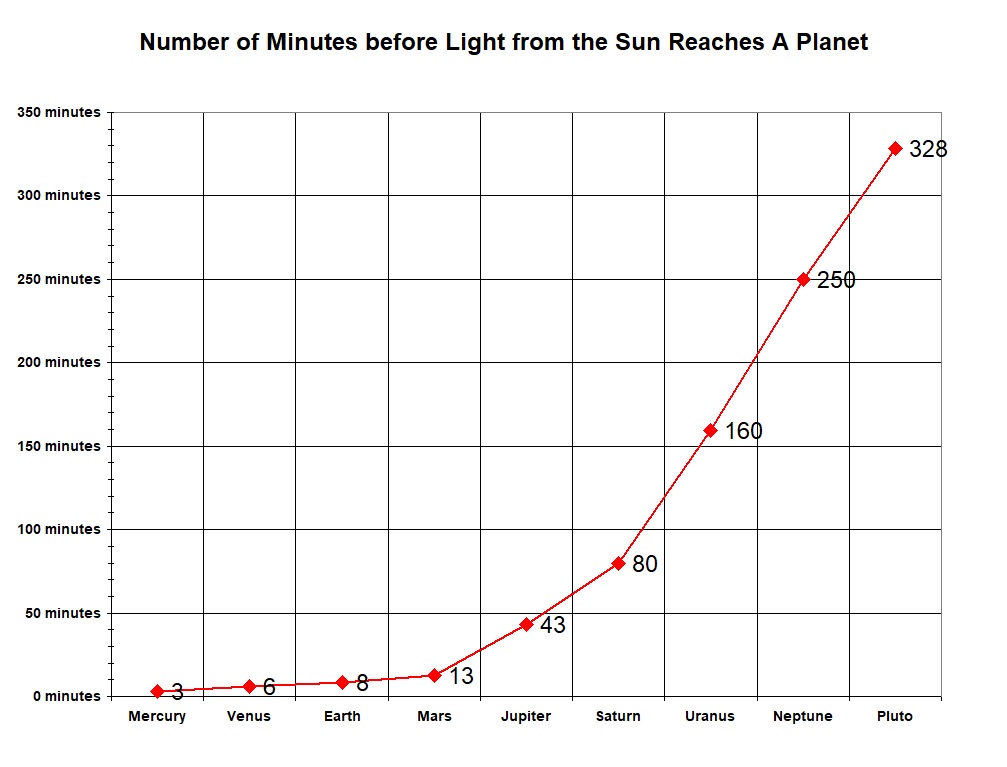
On a related note, and as illustrated in the table and chart below, light travels at a speed of 299,792 kilometers per second (times 60 seconds per minute = 17,987,547.48 kilometers per minute) or an equivalent of 186,282 miles per second (times 60 seconds per minute = 11,176,943.82 miles per minute). Take, Earth, for instance. Dividing by Earth's average distance from the Sun (that is, 149,597,870.7 ÷ 17,987,547.48 for kilometers or 92,955,807.24 ÷ 11,176,943.82 for miles), it follows that, on average, it takes 8.3 minutes for light to travel from the Sun to Earth.
Say, for instance, one day the Sun suddenly stopped shining. The table and chart below indicate that it would be at least 8 minutes later before Earth also would go dark—and freezing cold—due to a lack of sunlight.
AMOUNT OF TIME IT TAKES FOR LIGHT FROM THE SUN TO REACH A PLANET
| Heavenly Body |
Image |
Average Distance from Sun (Kilometers) |
Speed of Light (Kilometers Per Second) |
Speed of Light Per Minute (Kilometers) |
Average Distance from Sun (Miles) |
Speed of Light (Miles Per Second) |
Speed of Light Per Minute (Miles) |
Total Light Travel Time |
| Unit of Measurement |
 |
Kilometers |
Kilometers |
Kilometers |
Miles |
Miles |
Miles |
Minutes |
| Mercury |
 |
57,900,000 |
299,792 |
17,987,547.48 |
35,977,392 |
186,282 |
11,176,943.82 |
3.22 |
| Venus |
 |
108,200,000 |
299,792 |
17,987,547.48 |
67,232,363 |
186,282 |
11,176,943.82 |
6.02 |
| Earth |
 |
149,597,871 |
299,792 |
17,987,547.48 |
92,955,807 |
186,282 |
11,176,943.82 |
8.32 |
| Mars |
 |
227,900,000 |
299,792 |
17,987,547.48 |
141,610,495 |
186,282 |
11,176,943.82 |
12.67 |
| Jupiter |
 |
778,600,000 |
299,792 |
17,987,547.48 |
483,799,610 |
186,282 |
11,176,943.82 |
43.29 |
| Saturn |
 |
1,433,500,000 |
299,792 |
17,987,547.48 |
890,735,604 |
186,282 |
11,176,943.82 |
79.69 |
| Uranus |
 |
2,872,500,000 |
299,792 |
17,987,547.48 |
1,784,888,749 |
186,282 |
11,176,943.82 |
159.69 |
| Neptune |
 |
4,495,100,000 |
299,792 |
17,987,547.48 |
2,793,125,645 |
186,282 |
11,176,943.82 |
249.90 |
| Pluto |
 |
5,906,400,000 |
299,792 |
17,987,547.48 |
3,670,066,808 |
186,282 |
11,176,943.82 |
328.36 |
Herein lies the greatness of Sir Isaac Newton. It simply is inconceivable how he sat at his desk and proceeded to mathematically describe how the entire Universe works on a macro, physical, and mechanical level. Even more astonishing is, in so doing, how Sir Isaac Newton proceeded to create his own branch of mathematics better known as calculus—albeit Gottfried Leibniz also is credited with independently creating calculus. It was an amazing mental feat, and it inspired many generations of scientists to follow including the great Albert Einstein (who would later completely re-write Sir Isaac Newton's description of how the Universe works at a macro level).
Sir Isaac Newton's marvelous accomplishments are unrivaled, and they marked the triumph of science over superstition. Even today in these modern times, the numerous artificial satellites in orbit around Earth are the direct result of Sir Isaac Newton's contributions to science. In effect, the artificial satellites are made to orbit Earth in the same manner which Sir Isaac Newton mathematically described how and why the planets remain in orbit around the Sun. Much like the present-day generation of nuclear energy, for instance, the launching of artificial satellites into orbit around Earth more commonly is referred to as the use of applied mathematics.